Você já ouviu falar em algoritmo MDC, mas não sabe direito para que serve? Pois é, quando precisamos simplificar frações ou encontrar o maior divisor comum entre dois números, essa ferramenta é essencial. Fica tranquilo, porque neste post eu vou te mostrar como ele funciona na prática e como você pode usá-lo sem complicação.

Desvendando o MDC: A Chave Para Simplificar Cálculos

Você já se perguntou como os computadores simplificam números grandes para tornar tudo mais fácil? O segredo está no algoritmo MDC, o Máximo Divisor Comum. Ele encontra o maior número que divide dois ou mais números sem deixar resto. Pense nisso como achar a maior peça de um quebra-cabeça que se encaixa perfeitamente em todos os conjuntos de números que você tem.

Utilizar o MDC traz um monte de vantagens, principalmente na computação. Ele é essencial para simplificar frações, por exemplo, tornando cálculos mais rápidos e eficientes. Além disso, em áreas como a criptografia, ele ajuda a garantir a segurança das suas informações. É uma ferramenta matemática fundamental que faz um trabalho pesado nos bastidores da tecnologia que usamos todos os dias.

Confira este vídeo relacionado para mais detalhes:

Passo a Passo Descomplicado do Máximo Divisor Comum

Entendendo o Conceito de Divisor

Quando falamos de divisor, estamos nos referindo a um número inteiro que divide outro número inteiro sem deixar resto. Pensa assim: se o número 2 divide o número 10 perfeitamente, sem sobrar nada, então o 2 é um divisor de 10. O mesmo vale para o 5 e o próprio 10. É a base para um monte de operações e conceitos mais complexos, incluindo o famoso algoritmo MDC (Máximo Divisor Comum).

No contexto de algoritmos, como o MDC, entender divisores nos ajuda a encontrar o maior número que divide dois ou mais números simultaneamente. Isso tem aplicações práticas em diversas áreas, desde a organização de dados até a criptografia. Saber identificar os divisores de um número é como ter uma chave para decifrar certos padrões numéricos.

Dominar o conceito de divisor não é apenas teoria. É uma habilidade que simplifica a resolução de problemas. Se você está aprendendo sobre divisores ou sobre o algoritmo MDC, lembre-se que a prática leva à perfeição. Teste com diferentes números, procure padrões e você vai ver como fica mais fácil.

Dica Prática: Para encontrar rapidamente os divisores de um número, teste os números inteiros a partir de 1 até a raiz quadrada desse número. Se um número divide o original, o resultado da divisão também é um divisor.

Identificando os Divisores de um Número

Saber identificar todos os números que dividem outro número exatamente é o primeiro passo. Pensa assim: se você tem 12 balas, quais são as quantidades de pacotes que você pode fazer, sem sobrar nenhuma bala? Pode ser em pacotes de 1, 2, 3, 4, 6 ou 12 balas. Esses são os divisores de 12. A gente faz isso testando cada número a partir do 1 até chegar no próprio número. Se a divisão não deixa resto, achamos um divisor.

Quando falamos de “algoritmo mdc”, estamos falando do Máximo Divisor Comum. Isso é um pouco mais avançado, mas a base é justamente encontrar esses divisores. Para achar o MDC entre dois números, por exemplo, você lista todos os divisores de um, lista todos os divisores do outro, e depois vê qual é o maior número que aparece nas duas listas. Ferramentas e códigos computacionais fazem isso rapidinho, mas entender o conceito por trás é o que faz a diferença.

Dominar a identificação de divisores abre portas para entender funções matemáticas mais complexas e como elas são usadas em computação. É a base para muitos cálculos. Lembre-se que números primos, por exemplo, só têm dois divisores: o 1 e ele mesmo. Isso é uma característica que define um número primo e é importantíssimo em criptografia.

Dica Prática: Para encontrar os divisores de um número grande de forma mais rápida, não precisa testar todos os números até ele. Basta testar até a raiz quadrada do número. Se você achar um divisor ‘x’, automaticamente ‘número / x’ também será um divisor.

Listando os Divisores Comuns Entre Dois Números

Você já se pegou pensando quais números dividem dois outros números perfeitamente, sem deixar resto? É aí que entra a ideia de divisores comuns. Por exemplo, se você tem os números 12 e 18, os divisores de 12 são 1, 2, 3, 4, 6 e 12. Já os de 18 são 1, 2, 3, 6, 9 e 18. Olhando para as duas listas, a gente vê que 1, 2, 3 e 6 aparecem em ambas. Esses são os divisores comuns!

Quando a gente fala em encontrar esses divisores, especialmente para números maiores, um método bem prático é usar o conceito do algoritmo MDC, que significa Máximo Divisor Comum. Na verdade, encontrar o MDC já nos dá uma pista enorme sobre quais outros divisores são comuns. Pense assim: se você souber qual é o maior número que divide ambos, os outros divisores comuns serão simplesmente os divisores desse MDC. É uma maneira eficiente de organizar a busca, sabe?

Para simplificar tudo, você pode listar todos os divisores de um número e depois comparar com os divisores do outro. Ou, como mencionei, achar o MDC primeiro e depois listar os divisores dele. Isso ajuda muito a não se perder, principalmente se os números forem grandes. É um processo que agiliza o trabalho e evita erros.

Dica Prática: Para agilizar a listagem dos divisores de um número, basta testar a divisão dele por todos os números inteiros de 1 até a raiz quadrada desse número. Se a divisão for exata, você encontrou um par de divisores: o número que dividiu e o resultado da divisão.

Encontrando o Maior Divisor Comum (MDC)

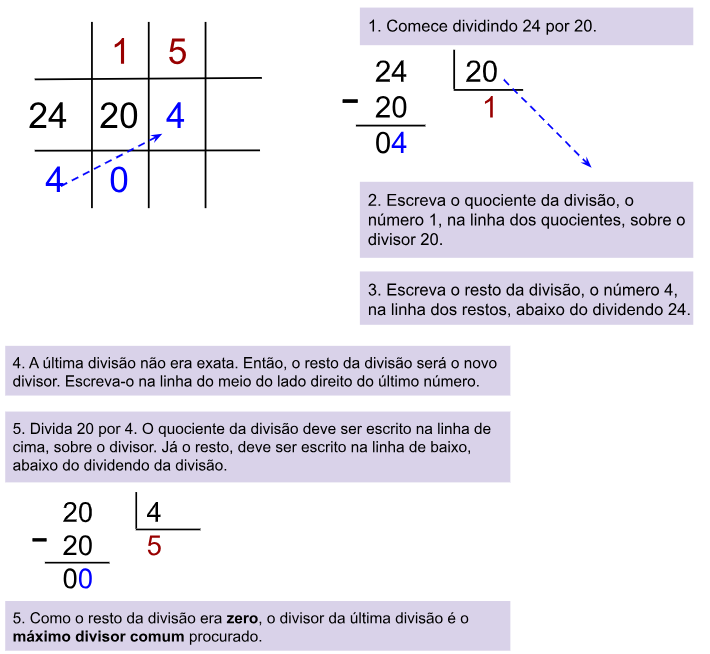
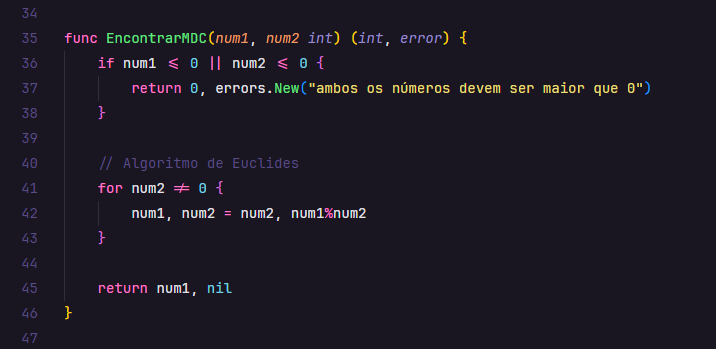
O mais conhecido e eficiente é o Algoritmo de Euclides. Ele funciona na base da divisão sucessiva. Você pega os dois números, divide o maior pelo menor e pega o resto. Aí, o menor vira o novo maior e o resto vira o novo menor. Repete isso até o resto ser zero. O último resto que não foi zero é o MDC. É um processo bem direto e que economiza bastante cálculo pro computador.

Para quem mexe com programação, dominar o algoritmo MDC é fundamental. Ele te ajuda a resolver problemas de forma mais elegante e com melhor performance. Se você está aprendendo a programar, tente implementar esse algoritmo em alguma linguagem que você curta. É um ótimo exercício prático.

Dica Prática: Ao simplificar frações no seu código, usar o MDC pode te poupar um trabalho danado e garantir que o resultado final esteja na forma mais reduzida possível.

Método da Divisão Sucessiva para o MDC

Você já se deparou com a necessidade de achar o maior número que divide dois outros números inteiros sem deixar resto? Esse é o tal do Máximo Divisor Comum, o MDC. Muita gente acha que é complicado, mas tem um jeito bem prático de fazer isso: a divisão sucessiva. É um método que funciona que é uma beleza para encontrar esse valor.

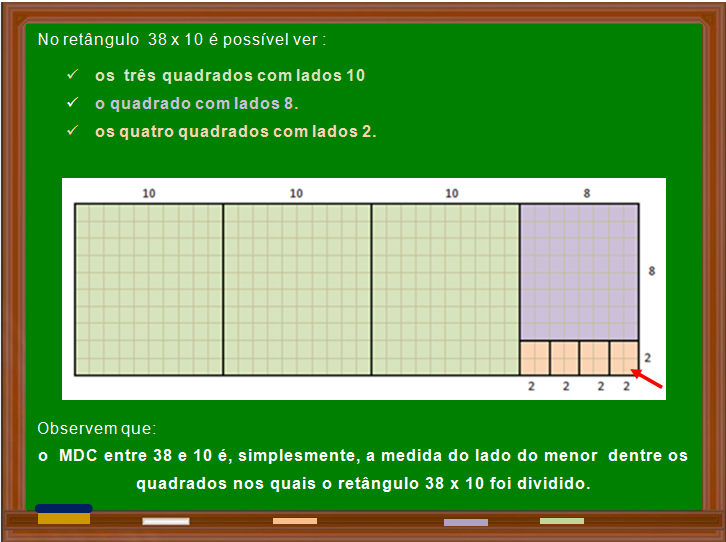
O segredo do algoritmo mdc por divisão sucessiva é bem simples. Você pega os dois números, divide o maior pelo menor. Se sobrar resto, você pega o divisor anterior e divide pelo resto. Repete esse processo. A hora que o resto der zero, o último divisor que você usou é o MDC. Parece um jogo de detetive, né? Cada passo te leva mais perto da resposta certa.

É um método eficiente e que você pode usar sempre que precisar. Não tem erro! Com um pouco de prática, você pega o jeito rapidinho e o MDC vira moleza.

Dica Prática: Se um dos números for zero, o MDC é o outro número. Simples assim!

Exemplo Prático: MDC de 24 e 36

Você quer saber qual o Maior Divisor Comum (MDC) entre 24 e 36? Pois é, esse tal de algoritmo MDC entra em ação para resolver isso de um jeito bem direto. Pensa comigo: o MDC é o maior número que divide dois ou mais números inteiros sem deixar resto. Ele é super útil em várias situações, desde simplificar frações até em problemas de organização. Vamos pegar esses dois números, 24 e 36, e ver como o algoritmo chega nessa resposta.

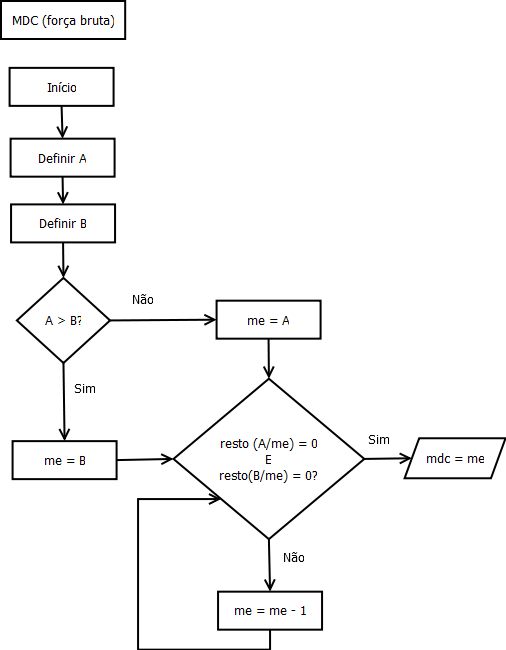
Para encontrar o MDC de 24 e 36 usando o algoritmo, a gente pode listar os divisores de cada número. Os divisores de 24 são: 1, 2, 3, 4, 6, 8, 12 e 24. Agora, os divisores de 36 são: 1, 2, 3, 4, 6, 9, 12, 18 e 36. Se você olhar com atenção, vai ver que os divisores comuns são 1, 2, 3, 4, 6 e 12. O maior deles? É o 12! Então, o MDC de 24 e 36 é 12.

Existem métodos mais eficientes que a listagem para calcular o MDC, como o Algoritmo de Euclides, que usa as divisões sucessivas. Mas, para entender a ideia básica, listar os divisores já ajuda bastante. Saber o MDC de dois números te permite, por exemplo, simplificar a fração 24/36. Dividindo ambos por 12, você chega a 2/3, que é a fração irredutível. Fica muito mais fácil trabalhar assim, não acha?

Dica Prática: Ao lidar com problemas de divisão onde você quer o maior número que divide ambos os lados igualmente, pense no MDC. Ele simplifica tudo!

MDC com Números Maiores: Fatoração em Primos

Muita gente pensa que calcular o Máximo Divisor Comum (MDC) de números grandes é um bicho de sete cabeças, mas a verdade é que existe um método bem esperto para isso: a fatoração em números primos. Sabe quando você decompõe um número em vários outros que, multiplicados, voltam a ser o original? É exatamente isso que vamos fazer aqui, mas com um objetivo específico para encontrar o MDC.

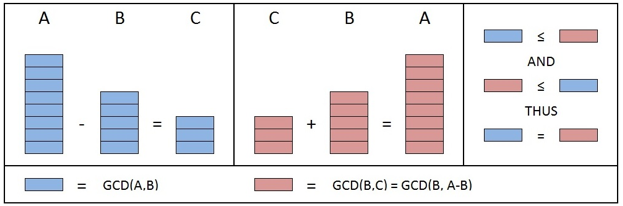
O segredo é fatorar cada um dos números em seus fatores primos. Depois, você olha para essas decomposições e seleciona apenas os fatores primos que aparecem em *todos* os números e que têm a *menor* potência. Multiplicando esses fatores comuns selecionados, você chega direto no MDC. É como achar os ingredientes que todos os seus números têm em comum para fazer a base do maior divisor.

Para números maiores, esse método se torna mais organizado do que a divisão sucessiva, especialmente se você já tem familiaridade com a decomposição em primos. Ajuda a visualizar quais são os “blocos de construção” que se repetem entre os números.

Dica Prática: Antes de sair fatorando números gigantes, pratique a decomposição em primos com números menores para pegar o jeito. Use uma lista dos primeiros números primos (2, 3, 5, 7, 11…) como guia para agilizar o processo.

Desmistificando o MDC com Três ou Mais Números

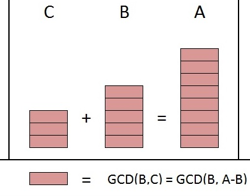
Pois é, o que muita gente não sabe é que o famoso algoritmo do MDC, aquele que a gente usa para dois números, pode ser aplicado em sequência. Se você quer achar o MDC de, digamos, A, B e C, você primeiro acha o MDC de A e B. Depois, pega esse resultado e acha o MDC dele com C. Esse número final é o MDC de todos eles. Viu só? É como ir descascando uma cebola, uma camada de cada vez. O conceito é o mesmo, só aplicamos mais de uma vez.

E a beleza disso é que essa abordagem vale para quantos números você precisar. Seja para quatro, cinco ou dez números, o processo se repete. Você vai calculando o MDC de dois em dois, usando o resultado anterior como um dos números para a próxima conta. É uma maneira bem eficiente de chegar ao resultado sem se perder.

Dica Prática: Para agilizar, use uma calculadora de MDC online para os primeiros passos se você estiver com pressa, mas tente fazer manualmente pelo menos uma vez para pegar o jeito do algoritmo. Isso te ajuda a fixar o processo.

Aplicações Reais do MDC no Dia a Dia

Pense em como você compartilha arquivos. Quando você envia uma foto ou um vídeo para alguém, o computador precisa “simplificar” essa informação para que ela viaje mais rápido pela internet. O MDC entra aí para reduzir o tamanho desses arquivos sem perder qualidade essencial. Ele ajuda a encontrar a “menor forma” de representar os dados, o que agiliza o download e o upload.

Essa ideia de simplificar e dividir sem sobras é o que o algoritmo MDC faz. Ele encontra o maior número que divide dois ou mais números sem deixar resto. É tipo um organizador super eficiente.

Dica Prática: Se você está lidando com planilhas e precisa dividir uma quantidade grande de itens em grupos iguais e do maior tamanho possível, use o MDC para descobrir o tamanho ideal de cada grupo.

Dicas Extras para Calcular o MDC Rapidamente

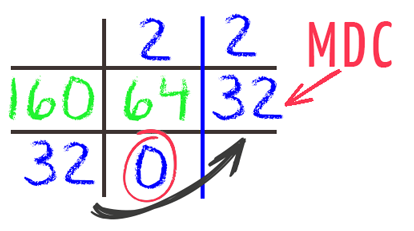
Quando você precisa achar o MDC de dois números, tipo 36 e 24, sem o algoritmo de Euclides, a gente acaba listando os divisores de cada um: divisores de 36 são 1, 2, 3, 4, 6, 9, 12, 18, 36. E os de 24 são 1, 2, 3, 4, 6, 8, 12, 24. Depois, a gente olha quais números aparecem nas duas listas e pega o maior deles. No caso, é o 12. Funciona, mas dá um trabalho, né?

Agora, com o algoritmo de Euclides, a coisa muda de figura. A ideia é usar a divisão. Você divide o número maior pelo menor e pega o resto. Se o resto for zero, o MDC é o divisor. Se não for zero, você repete o processo, dividindo o divisor pelo resto. Vamos fazer com 36 e 24: 36 dividido por 24 dá 1, com resto 12. Como o resto não é zero, a gente divide 24 por 12. Dá 2, com resto zero! Pronto, o MDC é 12. Viu como é mais direto?

Esse método é super útil, especialmente com números maiores. Ele é um processo repetitivo que vai te levar à resposta sem dor de cabeça. É uma ferramenta matemática que vale a pena ter na sua caixinha de ferramentas digitais, digamos assim. É a prova de que nem tudo na matemática é complicado!

Dica Prática: Se você estiver usando o computador, pode procurar por “algoritmo MDC” em sites de matemática ou até em calculadoras online avançadas. Elas costumam ter implementações que fazem isso para você em segundos.

Onde o MDC Aparece no Seu Mundo?

Item	O Que Significa	Como Funciona (Simplificado)	Dica Rápida do Autor
Entendendo o Conceito de Divisor	Um divisor é um número que divide outro número sem deixar resto. Pense nele como um pedaço exato.	Se 12 dividido por 3 dá 4, então 3 é divisor de 12.	Todo número tem 1 e ele mesmo como divisores. Fácil, né?
Identificando os Divisores de um Número	É listar todos os números que dividem um número específico exatamente.	Para 10: 1, 2, 5, 10. Faça divisões até chegar na metade do número, depois confira os pares.	A dica é: comece sempre com 1 e o próprio número. Depois, vá testando os pequenos.
Listando os Divisores Comuns Entre Dois Números	São os números que aparecem na lista de divisores de dois ou mais números.	Divisores de 12: 1, 2, 3, 4, 6, 12. Divisores de 18: 1, 2, 3, 6, 9, 18. Comuns: 1, 2, 3, 6.	Depois de listar os divisores de cada um, é só circular os que se repetem. Simples assim.
Encontrando o Maior Divisor Comum (MDC)	É o maior número que divide dois ou mais números ao mesmo tempo.	No exemplo anterior (12 e 18), o maior divisor comum é o 6.	É o “vencedor” da lista de divisores comuns. O maior de todos!
Método da Divisão Sucessiva para o MDC	Um jeito rápido e eficaz de achar o MDC, especialmente quando os números são grandes.	Divida o maior pelo menor. Pegue o resto e divida o menor. Repita até o resto ser zero. O último divisor usado é o MDC.	Esse método é ouro! Poupa um tempo danado e evita erros. Confia em mim.
Exemplo Prático: MDC de 24 e 36	Vamos colocar a mão na massa para entender de vez.	Divisão sucessiva: 36 ÷ 24 = 1 (resto 12). Agora: 24 ÷ 12 = 2 (resto 0). O último divisor foi 12. MDC(24, 36) = 12.	Viu como é direto? O segredo é não se perder nos passos.
MDC com Números Maiores: Fatoração em Primos	Para números maiores, decompor em fatores primos ajuda a visualizar o MDC.	24 = 2³ × 3. 36 = 2² × 3². Pegue os fatores primos comuns com o menor expoente: 2² × 3 =

Confira este vídeo relacionado para mais detalhes:

Evitando Armadilhas Comuns ao Calcular o MDC

Calcular o Máximo Divisor Comum (MDC) pode parecer simples, mas algumas pegadinhas podem te fazer perder tempo. Eu já passei por isso e quero te dar umas dicas para facilitar sua vida.

Fica tranquilo, com essas orientações você vai calcular o MDC sem dor de cabeça:

• Não confunda com MMC: Essa é clássica! O MDC busca o maior número que divide *ambos* os números. Já o Mínimo Múltiplo Comum (MMC) busca o menor número que é *múltiplo* de ambos. São objetivos opostos, sacou?
• Priorize a fatoração: Quando os números são maiores, tentar dividir um por um pode ser cansativo. A fatoração em primos é o caminho mais seguro. Decomponha cada número em seus fatores primos e pegue apenas os fatores que aparecem *em comum*, multiplicando-os.
• Um número divide o outro? Se um dos números que você quer calcular o MDC é um divisor do outro, o MDC é o próprio menor número. Exemplo: MDC de 6 e 12 é 6. Simples assim!
• E se um for 1? O MDC de qualquer número com 1 é sempre 1. Não tem erro.

Vamos combinar, aplicar essas dicas faz toda a diferença. Na hora de resolver um problema ou mesmo para entender a lógica por trás de um código, saber essas manhas te deixa um passo à frente.

Dúvidas das Leitoras

Pratique e Domine o Cálculo do MDC

O que é exatamente um algoritmo MDC?

Um algoritmo MDC é um conjunto de passos lógicos para encontrar o Maior Divisor Comum entre dois ou mais números. É como uma receita que te guia para achar esse número especial.

Por que é importante saber calcular o MDC?

Saber calcular o MDC é fundamental para simplificar frações e resolver diversos problemas em matemática e computação. Facilita muito a vida em cálculos mais complexos.

Existe um jeito mais fácil de achar o MDC?

Sim, o algoritmo de Euclides é um método bem eficiente e rápido para calcular o MDC. Ele usa o resto das divisões sucessivas e é bem mais prático que listar todos os divisores.

O MDC serve só para matemática ou tem outras utilidades?

Pois é, o MDC aparece em várias áreas! Na computação, por exemplo, ele é usado em algoritmos de criptografia e compressão de dados. Ele tem seu valor fora da sala de aula!

Entender o algoritmo MDC é fundamental para quem trabalha com programação e matemática. Ele resolve problemas de forma eficiente. Se você gostou disso, vale a pena ver também sobre números primos…

Compartilhe sua experiência ou deixe seu comentário!