Você já se perguntou como a mágica do algoritmo multiplicação acontece? Pois é, parece complexo, mas essa sequência de passos é a chave para desvendar produtos de números. Na escola, aprendemos um método que, muitas vezes, gera dúvidas. Mas a boa notícia é que estou aqui para te mostrar o caminho, descomplicando o que parece difícil e revelando como dominar essa ferramenta essencial em 2026. Prepare-se para uma nova perspectiva!
“A multiplicação longa envolve multiplicar as unidades, dezenas e centenas separadamente, com “transporte” quando o resultado excede nove.”
Entenda o Algoritmo de Multiplicação Usual Passo a Passo para Multiplicar Facilmente
Vamos combinar: entender o algoritmo de multiplicação é crucial para qualquer pessoa que lida com números, seja nos estudos ou no dia a dia. Ele é a base para realizar contas que vão além da simples adição.
O método mais conhecido, a multiplicação longa, que você aprendeu na escola, nada mais é que uma forma organizada de somar parcelas repetidas. Cada dígito do multiplicador atua sobre o multiplicando, gerando um resultado parcial. Ao final, somamos tudo isso para chegar ao produto final.
Dominar esse processo garante mais agilidade e confiança na hora de calcular. Você ganha uma ferramenta poderosa para resolver problemas práticos e até para otimizar tarefas mais complexas.
Desmistificando o Algoritmo de Multiplicação: a Base dos Cálculos
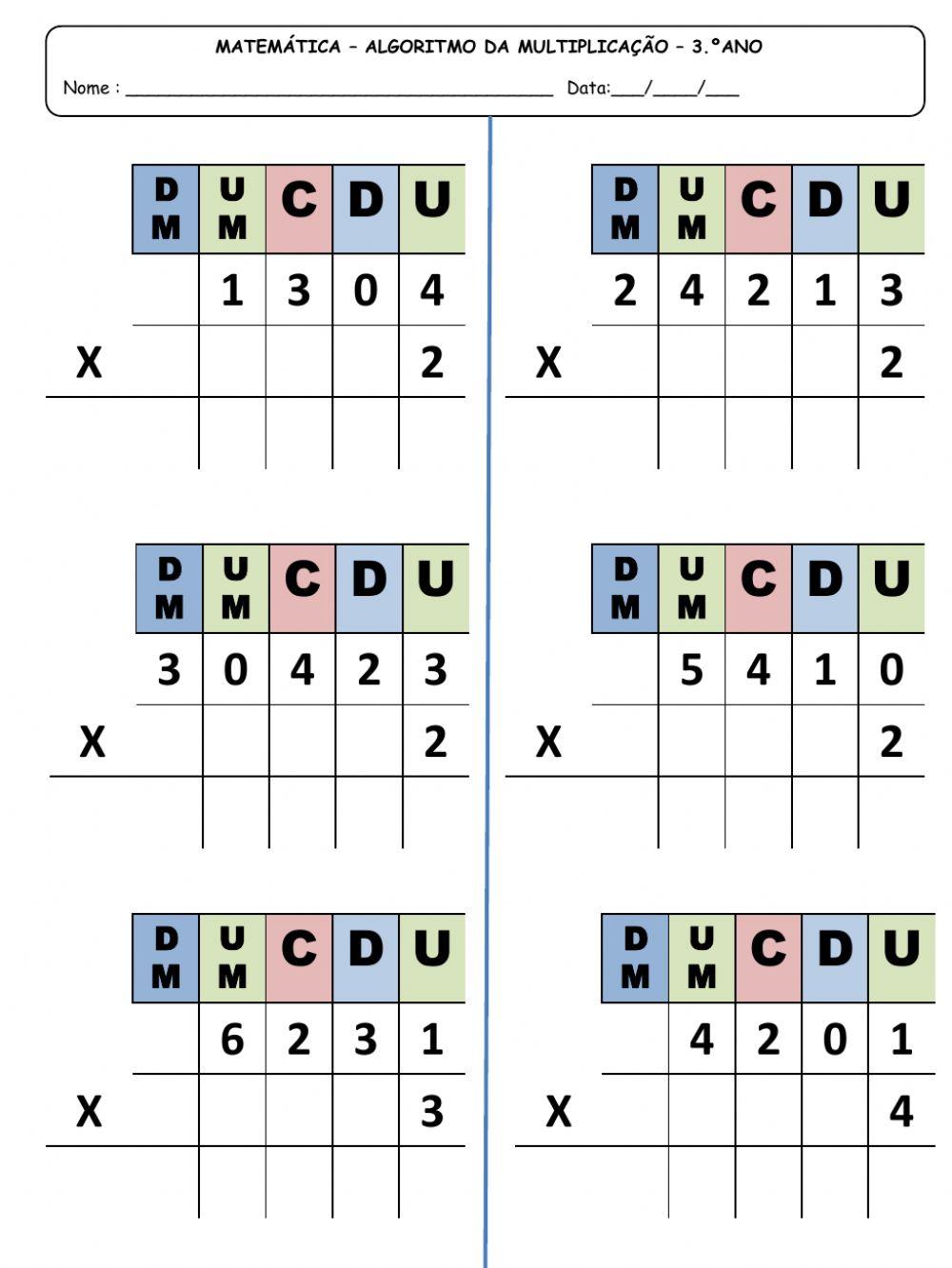
O algoritmo de multiplicação é, na sua essência, uma sequência organizada de passos lógicos que nos permite descobrir o produto (o resultado) de dois ou mais números. Pense nele como a receita de bolo dos números. Na matemática que aprendemos na escola, a ideia central é multiplicar cada algarismo de um número pelos algarismos do outro, e depois somar esses resultados parciais. Imagina!
| Conceito | Aplicação Escolar |
|---|---|
| Sequência lógica para encontrar o produto de números. | Multiplica algarismos individuais e soma os resultados parciais. |
Ferramentas Essenciais para Dominar a Multiplicação
Calculadora Científica Texas Instruments TI-30X IIS

Para quem precisa de precisão e recursos avançados, uma calculadora como a Texas Instruments TI-30X IIS é uma mão na roda. Ela não só executa multiplicações complexas com facilidade, mas também ajuda a conferir seus resultados manuais, garantindo que você esteja no caminho certo. É um item que te dá confiança.
Caderno Quadriculado e Lápis de Grafite
Não subestime o poder do papel e lápis! Um bom caderno quadriculado é fundamental para armar os números corretamente, garantindo alinhamento e facilitando a visualização dos passos do algoritmo usual. O lápis permite corrigir eventuais deslizes sem deixar a página uma bagunça. Essencial para aprender o ‘sobe um’ sem estresse.
Software de Planilha Eletrônica (Ex: Microsoft Excel ou Google Sheets)
Para aplicações práticas e até mesmo para verificar grandes volumes de cálculos, planilhas como o Microsoft Excel ou Google Sheets são imbatíveis. A função `MULTIPLICAR` (ou `PRODUCT` em inglês) faz o trabalho pesado, mas o legal é usar as fórmulas para replicar os passos do algoritmo, entendendo a lógica por trás.
Recursos Online de Apoio (Ex: Khan Academy)

Plataformas como a Khan Academy oferecem tutoriais em vídeo e exercícios práticos que detalham cada etapa do algoritmo de multiplicação. Ver exemplos visuais, como os encontrados em canais do YouTube, pode solidificar seu entendimento e te dar diferentes perspectivas sobre o tema.
Preparando-se para Multiplicar com Segurança
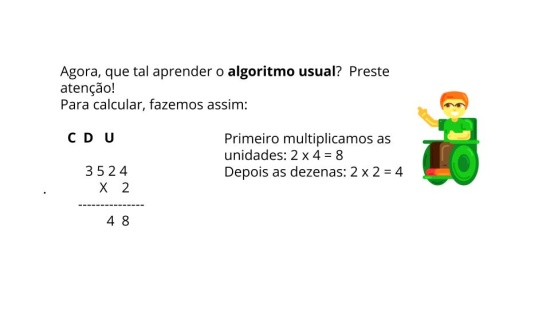
Antes de sair multiplicando, é crucial ter uma base sólida. Certifique-se de que você entende bem os conceitos de valor posicional (unidades, dezenas, centenas) e as operações de soma. Uma boa revisão da tabuada também acelera o processo e diminui a chance de erros bobos. Fica tranquila, é um passo que faz toda a diferença.
Como Fazer Multiplicações Passo a Passo: O Algoritmo Usual na Prática
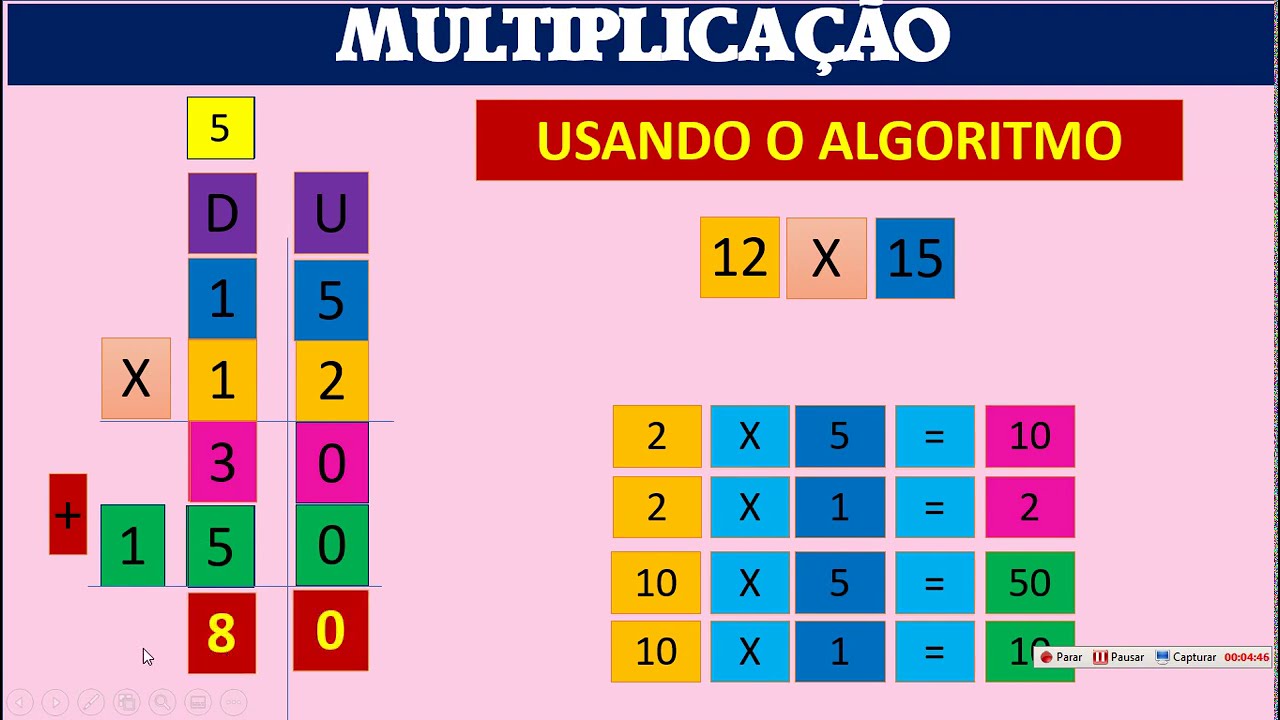
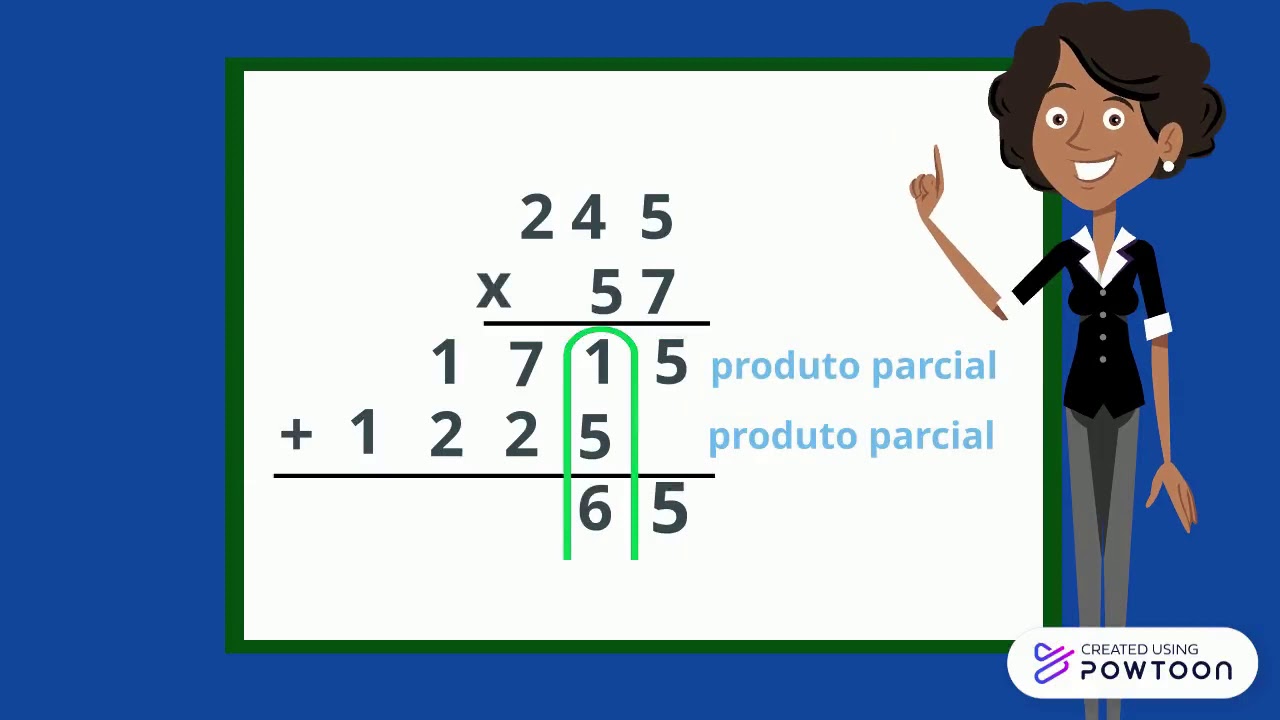
Vamos pegar o exemplo clássico de multiplicar 27 por 56. Este é o método que você provavelmente aprendeu na escola, o famoso ‘armar a conta’.
-
Multiplicação da Unidade: Começamos multiplicando o algarismo das unidades do segundo número (o 6 em 56) por todo o primeiro número (27). Assim:
- 6 multiplicado por 7 (unidades de 27): 6 x 7 = 42. Escrevemos o 2 embaixo e ‘subimos’ o 4 (o famoso ‘vai um’).
- 6 multiplicado por 2 (dezenas de 27): 6 x 2 = 12. Somamos o 4 que subiu: 12 + 4 = 16. Escrevemos o 16.
O primeiro resultado parcial é 162.
-
Deslocamento para a Próxima Casa: Agora, vamos multiplicar pelo algarismo das dezenas do segundo número (o 5 em 56). Como o 5 representa 50, precisamos ‘deslocar’ o resultado para a esquerda. Na linha de baixo, abaixo do 2 (a unidade do 162), colocamos um zero (ou simplesmente deixamos o espaço em branco), indicando que estamos multiplicando pela dezena.
-
Multiplicação da Dezena: Multiplicamos o 5 por todo o 27:
- 5 multiplicado por 7 (unidades de 27): 5 x 7 = 35. Escrevemos o 5 abaixo do 6 (lembre-se do zero na casa das unidades) e subimos o 3.
- 5 multiplicado por 2 (dezenas de 27): 5 x 2 = 10. Somamos o 3 que subiu: 10 + 3 = 13. Escrevemos o 13.
O segundo resultado parcial é 1350 (representado pelos algarismos 135, com o zero inicial implícito).
-
Soma Final dos Resultados Parciais: Por fim, somamos os dois resultados que encontramos: 162 + 1350. O resultado final é 1512. Pois é, 27 x 56 = 1512.
Como Consertar Erros Comuns na Multiplicação
Erros acontecem, o importante é saber identificá-los. Um dos mais comuns é esquecer de somar o número que ‘subiu’ (o ‘vai um’). Sempre revise se você incluiu esses valores nas multiplicações seguintes. Outro ponto é o alinhamento: se as casas decimais não estiverem bem organizadas, a soma final ficará incorreta. Use o caderno quadriculado! Se estiver usando um computador, lembre-se que algumas linguagens de programação, como o VBA no Excel, permitem simular esses cálculos passo a passo, ajudando a entender onde o erro pode ter ocorrido. A prática com diferentes métodos, como o algoritmo de decomposição, também pode clarear as ideias se o método usual estiver confuso.
Dicas de Ouro Para Dominar a Multiplicação
Vamos combinar, às vezes a multiplicação pode parecer um bicho de sete cabeças, né? Mas relaxa, eu tenho umas dicas que vão te dar um gás:
- Pratique com Números Pequenos Primeiro: Antes de se jogar nos números gigantes, mande ver com multiplicações mais simples. Isso ajuda a fixar o raciocínio sem se perder nos cálculos.
- Visualize o Processo: Tenta desenhar os passos. Coloca os números um embaixo do outro, alinha direitinho. Ver o passo a passo no papel faz toda a diferença para entender o que está acontecendo.
- Entenda o Significado: Lembra que multiplicar é somar repetidas vezes? Entender essa lógica por trás do algoritmo ajuda a não cair em decoreba.
- Revise a Tabuada: Pois é, a velha e boa tabuada é a base de tudo. Se ela estiver afiada, a multiplicação longa fica muito mais rápida e segura.
- Use a Tecnologia a Seu Favor (com Cautela): Calculadoras são ótimas para conferir, mas não dependa delas para aprender. Use-as para validar o seu resultado depois de fazer o cálculo manualmente.
- Divida para Conquistar: Se o número for muito grande, pensa em decompor. Separar em partes menores torna a conta mais gerenciável.
FAQ: Tirando Suas Dúvidas Sobre Algoritmos de Multiplicação
Sei que podem surgir perguntas no caminho. Vamos responder às mais comuns:
- O que é o ‘vai um’ na multiplicação longa?
- O ‘vai um’ (ou ‘vai o resto’) acontece quando a multiplicação de um algarismo pelo outro resulta em um número maior que 9. Você anota a unidade e ‘vai’ a dezena para somar com o próximo resultado parcial. É a forma de carregar o valor para a próxima casa decimal.
- Qual a diferença entre o algoritmo usual e a decomposição?
- O algoritmo usual (longa) é mais direto, multiplicando algarismo por algarismo e somando. A decomposição quebra os números em unidades, dezenas, centenas, etc., e multiplica essas partes separadamente antes de somar tudo. É mais intuitivo para entender o valor posicional, mas pode exigir mais passos.
- O algoritmo de Karatsuba é muito mais difícil?
- Ele é mais complexo que o usual, sim. Karatsuba é para quem já domina a multiplicação básica e quer otimizar o cálculo com números bem grandes. Ele usa uma abordagem esperta para reduzir o número de multiplicações necessárias.
- Por que o algoritmo de Booth é só para binários?
- Porque o sistema binário tem regras de sinal e representação de números negativos específicas. O algoritmo de Booth foi desenvolvido para lidar eficientemente com essas particularidades, otimizando a multiplicação em computadores, que trabalham com 0 e 1.
Conclusão: Multiplicar é Construir Ponte
Imagina só: aprender um algoritmo de multiplicação é como ganhar uma ferramenta nova e poderosa. Você sai do ‘eu não sei’ para o ‘eu consigo!’, seja somando repetidamente ou usando métodos mais elaborados.
Dominar esses passos não é só sobre acertar a conta. É sobre desenvolver o raciocínio lógico, a organização e a precisão. Cada multiplicação que você faz fortalece sua capacidade de resolver problemas, não só na matemática, mas na vida.
Então, bora praticar? Cada número que você desbrava te deixa mais confiante e pronto para os desafios que vêm pela frente. Continue explorando, continue calculando!

