Quando falamos de otimizar sistemas e aplicativos em 2026, um dos maiores gargalos que encontro no dia a dia são as limitações de performance causadas por estruturas de dados ineficientes. É aí que entram as fascinantes árvores em estrutura de dados. Muitos desenvolvedores sabem que elas existem, mas poucos dominam como usá-las para transformar lentidão em agilidade. Neste guia, vou te mostrar exatamente como você pode aplicar o poder das árvores para resolver problemas complexos e elevar a performance do seu código, de uma vez por todas.
“Cada nó em uma árvore binária pode ter, no máximo, dois filhos (esquerdo e direito).”
Desvendando as Árvores em Estrutura de Dados: O Que São e Por Que Você Precisa Saber em 2026
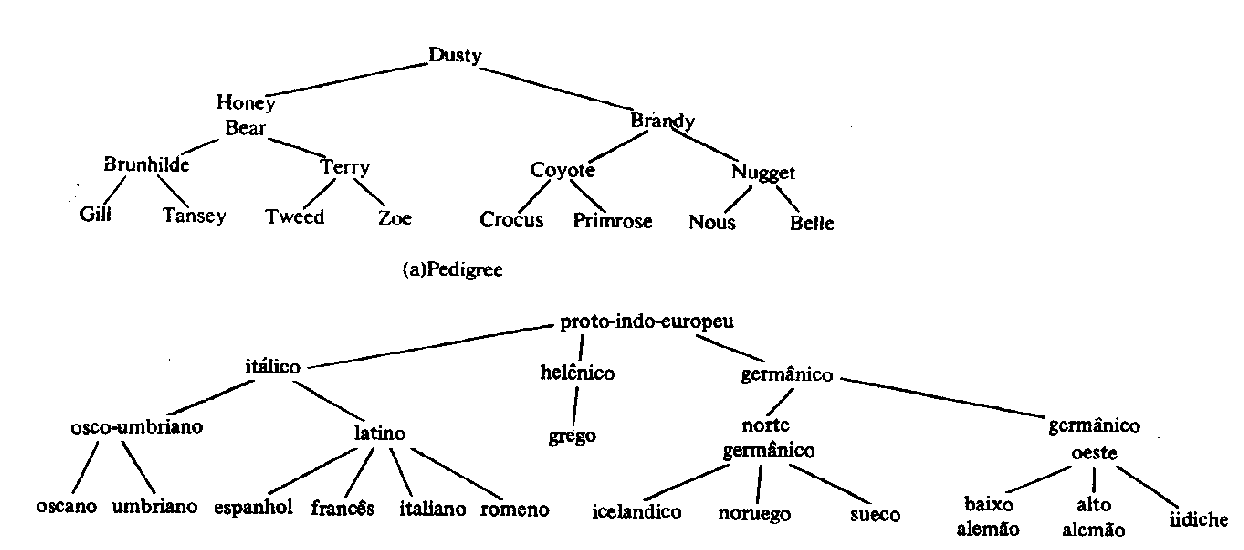
Imagina um organograma, mas para dados. É mais ou menos isso. As árvores são estruturas não lineares, perfeitas para organizar informações que têm uma relação de hierarquia, de cima para baixo.
Ao contrário de listas ou pilhas, onde os dados ficam em fila, as árvores se ramificam. Essa arquitetura é o segredo por trás de muitas otimizações.
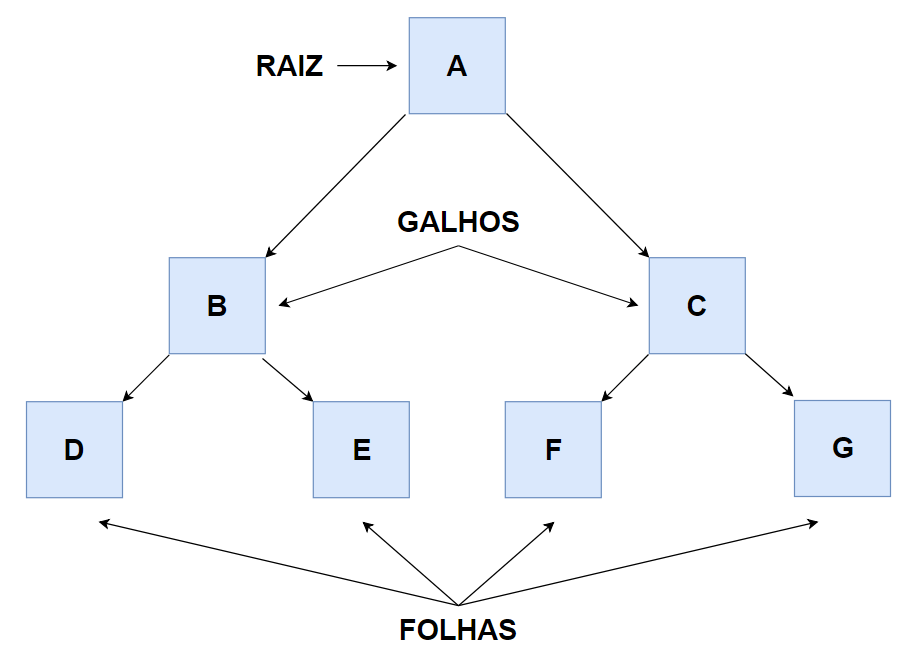
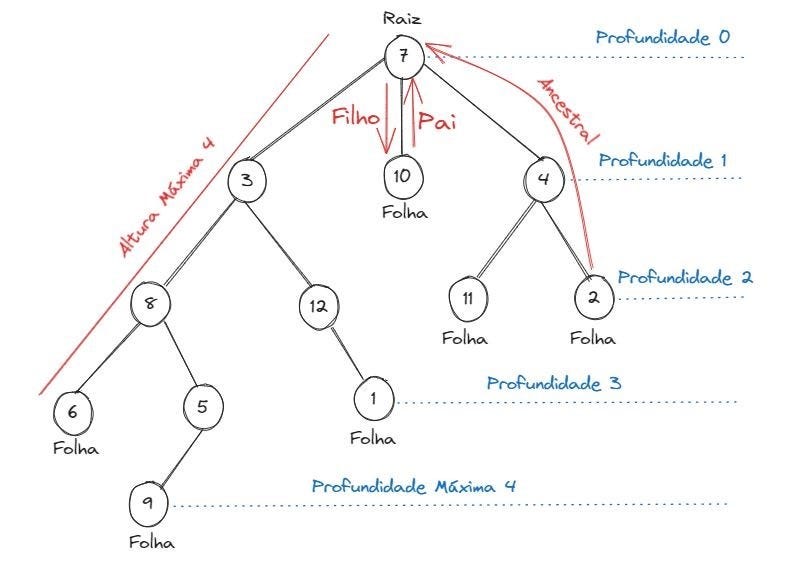
O ponto de partida de tudo é o nó raiz, o ancestral de todos os outros. Dele, partem os ramos que levam aos outros nós, chamados de filhos.
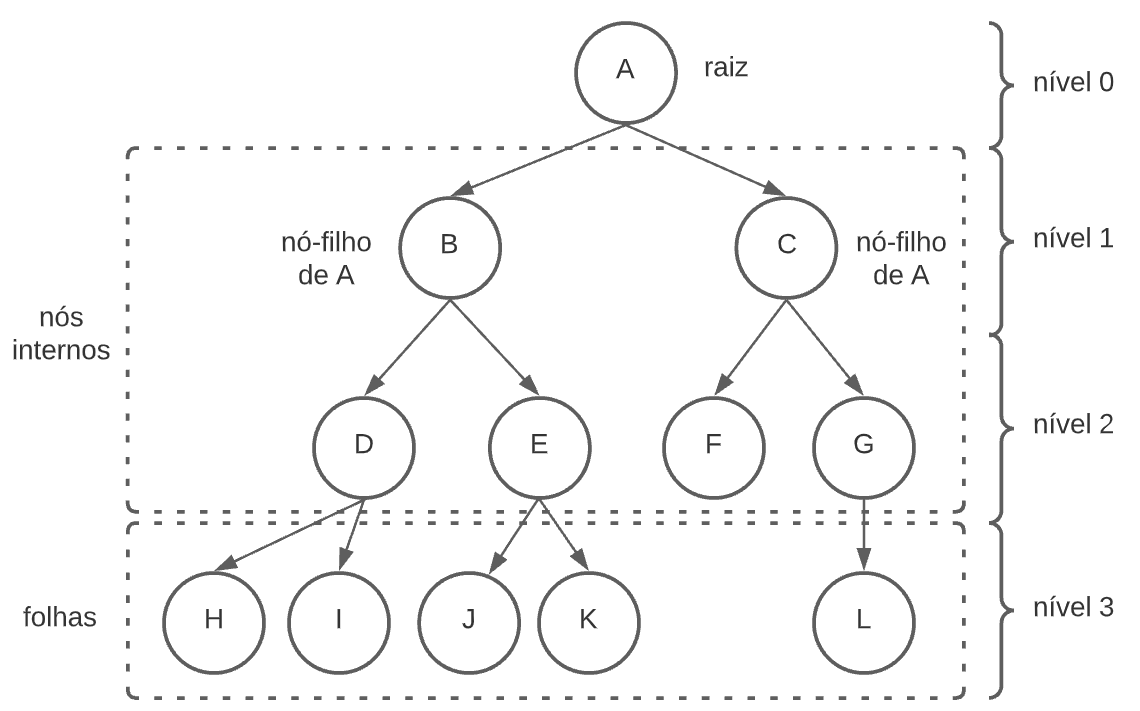
Cada nó, exceto as folhas (aquelas sem descendentes), tem um nó pai acima. Essa conexão pai-filho define a estrutura hierárquica.
Conceitos como altura e profundidade nos ajudam a entender a distância de um nó até a raiz ou até uma folha, o que é crucial para analisar a eficiência.
Entendendo o Conceito Principal de Árvores em Estruturas de Dados: A Hierarquia Direta ao Ponto
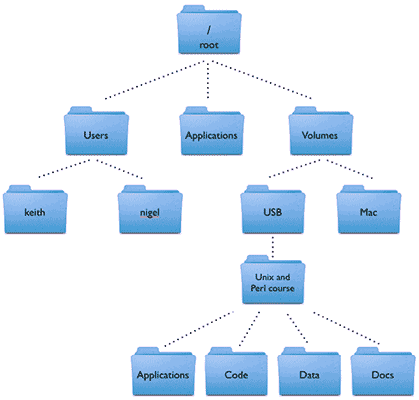
Imagina só, você está lidando com dados que têm uma relação de chefia e subordinação, tipo um organograma de empresa ou a pasta principal com todas as suas subpastas num computador. É aí que entram as árvores em estruturas de dados. Elas são como um diagrama invertido, onde tudo começa com um nó principal, a raiz, e dele saem ramificações para outros nós, que chamamos de filhos. Cada nó pode ter vários filhos, formando uma estrutura não linear e hierárquica. Ao contrário de listas ou pilhas, que são sequenciais, as árvores mostram essa relação de ‘quem é filho de quem’ de um jeito muito mais claro e eficiente.
| Termo | Descrição |
|---|---|
| Raiz | O nó inicial, topo da estrutura. |
| Nó Pai | O nó que contém uma conexão direta para outro nó. |
| Nó Filho | Um nó diretamente conectado a um nó pai. |
| Folha | Nó sem filhos, no final de um ramo. |
| Altura | Maior caminho entre a raiz e uma folha. |
| Profundidade | Caminho de um nó específico até a raiz. |
| Árvore Binária | Cada nó tem no máximo dois filhos (esquerdo e direito). |
| Árvore Binária de Busca (BST) | Organizada para buscas eficientes: menor à esquerda, maior à direita. |
| Árvores Balanceadas (AVL, Rubro-Negra) | BSTs que se autoajustam para manter a altura mínima, garantindo performance. |
| Trie (Árvore Digital) | Especializada para strings e buscas de prefixo. |
Materiais Essenciais para Explorar Árvores em Estruturas de Dados
Livro ‘Introduction to Algorithms’ (CLRS)
Se você quer aprofundar mesmo, o CLRS é uma referência. Ele explica as árvores de forma bem detalhada, cobrindo desde os conceitos básicos até os algoritmos mais complexos, como as árvores AVL e Rubro-Negras. É um material denso, mas fundamental para quem busca maestria. As explicações sobre a complexidade de tempo em operações são particularmente valiosas, algo que encontrei na seção de introdução a algoritmos.
Documentação Oficial do Python para Estruturas de Dados
Para quem programa em Python, a documentação oficial é um prato cheio. Ela detalha como as estruturas de dados, incluindo implementações de árvores, funcionam internamente e como usá-las da melhor forma. É uma fonte direta e confiável, sem rodeios. Abordam desde listas até estruturas mais complexas, como tutoriais sobre estruturas de dados.
Plataformas de Ensino Interativo: GeeksforGeeks e LeetCode
Para a prática, não tem jeito melhor. Plataformas como GeeksforGeeks e LeetCode oferecem explicações claras e exemplos de código em várias linguagens. O mais legal é que você pode testar os algoritmos diretamente no navegador. É onde eu mesmo costumo verificar implementações e entender melhor os conceitos de árvores na prática.
Artigos sobre Árvores B e B+ em Bancos de Dados
Para entender como as árvores são usadas em larga escala, buscar artigos específicos sobre indexação em bancos de dados é fundamental. As Árvores B e B+ são a espinha dorsal para acesso rápido a grandes volumes de dados. Uma leitura aprofundada sobre essas estruturas pode ser encontrada em artigos que discutem b-trees e otimização de consultas.
Preparando o Terreno: O Que Saber Antes de Mergulhar em Árvores
Antes de sair montando sua primeira árvore, é bom ter uma base sólida em alguns conceitos. Conhecer bem o que são ponteiros ou referências em programação é crucial, pois é assim que os nós se conectam. Entender sobre recursão também ajuda muito, já que muitas operações em árvores são naturalmente recursivas. Se você ainda tem dúvidas sobre como manipulação de memória funciona, recomendo dar uma olhada em recursos que explicam o que são ponteiros. Ah, e ter uma noção básica de complexidade de algoritmos (Big O notation) vai te ajudar a entender por que uma estrutura de árvore é melhor que outra em certos cenários.
Como Construir e Navegar em uma Árvore Binária: Passo a Passo Detalhado
-
Definir a Estrutura do Nó
Primeiro, você precisa definir como será um nó individual. Pense nele como uma caixinha que guarda um valor e aponta para onde estão seus filhos. Em linguagens como C, isso seria uma struct com um campo para o dado e ponteiros para os filhos. Em Python, seria uma classe. Vou te mostrar um exemplo simplificado, imaginando cada nó com um valor e, no máximo, um filho à esquerda e um à direita.
-
Criar o Nó Raiz
A árvore começa com a raiz. Geralmente, você aloca memória para o primeiro nó e o designa como a raiz da sua árvore. Se a árvore estiver vazia, a raiz é nula.
-
Inserir Novos Nós
Para inserir um novo nó, você geralmente começa na raiz. Para uma Árvore Binária de Busca (BST), você compara o valor do novo nó com o valor do nó atual. Se for menor, vai para a esquerda; se for maior, vai para a direita. Repete esse processo até encontrar um lugar vazio para inserir o novo nó. Essa lógica pode ser implementada de forma recursiva ou iterativa. É um processo que exige atenção aos detalhes, pois um erro pode levar a uma estrutura desbalanceada.
-
Percorrer a Árvore (Travessia)
Existem várias maneiras de visitar todos os nós. As mais comuns são:
- Pré-ordem: Visita a raiz primeiro, depois o subárvore esquerda e por último a direita. Pense em processar o ‘pai’ antes dos ‘filhos’.
- Em-ordem (Simétrica): Visita a subárvore esquerda, depois a raiz e, por fim, a direita. Se for uma BST, essa ordem te dá os elementos de forma classificada. É útil para relatórios ordenados, sabe?
- Pós-ordem: Visita a subárvore esquerda, depois a direita e só então a raiz. Útil, por exemplo, para deletar nós sem perder referências.
- Busca em Largura (BFS): Visita os nós camada por camada, da esquerda para a direita. Funciona como um ‘varredor’.
Cada método tem seu propósito e é escolhido dependendo do que você quer fazer com os dados. Entender qual usar é chave para otimizar seu código, como vi em algumas discussões sobre algoritmos de travessia de árvore.
-
Buscar um Nó Específico
A busca numa BST é onde a mágica acontece. Você começa na raiz e, dependendo do valor que procura, decide se vai para a esquerda ou para a direita. Isso repete até achar o valor ou perceber que ele não existe na árvore. É muito mais rápido do que varrer uma lista inteira, especialmente com muitos dados. Essa eficiência é o motivo de serem usadas em indexação de dados, como em formatos como BSON que podem se beneficiar de estruturas de busca rápidas.
Como Corrigir Erros Comuns ao Trabalhar com Árvores
Pois é, trabalhar com árvores pode ter suas armadilhas. Um erro bem comum é a perda de referência quando você está deletando ou movendo nós. Se você não gerenciar bem os ponteiros, pode acabar com ‘lixo’ de memória ou, pior, com uma árvore quebrada. Outro ponto é o balanceamento: árvores que crescem muito para um lado só (como uma BST não balanceada) podem se tornar tão lentas quanto listas. Por isso, o uso de árvores balanceadas como AVL ou Rubro-Negra é recomendado em aplicações críticas, garantindo que a altura da árvore permaneça controlada. Se você notar que suas operações estão lentas, pode ser um sinal de que sua árvore precisa ser reestruturada ou que você deveria ter optado por um tipo de árvore mais robusto. Para se aprofundar, recomendo ler sobre árvores AVL e suas propriedades de balanceamento. E se você estiver implementando em C, tome cuidado redobrado com alocação dinâmica de memória para evitar vazamentos.

