Enfrentando desafios complexos em busca de caminhos ideais? O algoritmo A* é a resposta que você procura. Muitos se perdem em métodos que exploram todas as possibilidades sem foco, gastando tempo e recursos preciosos. Neste guia completo de 2026, vou te mostrar como o A* otimiza essa jornada, garantindo que você encontre o destino mais eficiente, direto ao ponto. Prepare-se para uma busca inteligente.
“O algoritmo A* utiliza a função f(n)=g(n)+h(n), onde g(n) é o custo real do início até o nó atual e h(n) é uma estimativa do custo do nó atual até o destino.”
Como o Algoritmo A* Garante o Caminho Mais Curto de Forma Inteligente?
O A* é um mestre em planejamento de rotas.
Ele combina o que você já gastou para chegar a um ponto com uma previsão do quanto falta.
Assim, sempre foca no caminho com menor custo total aparente.
Isso o torna muito mais rápido que métodos que exploram tudo.
Algoritmo A* (A-Estrela): Desvendando o Caminho Mais Curto com Busca Inteligente
Olha só, o algoritmo A* (ou A-estrela, como a gente chama) é um dos craques quando o assunto é encontrar o trajeto ideal, sabe? Ele serve para achar o caminho mais curto entre um ponto de partida e um destino, sendo super usado em sistemas de navegação e até em jogos. Pense nele como um cruzamento eficiente entre a precisão do Dijkstra e a agilidade de uma busca informada. Diferente das buscas ‘cegas’, que exploram tudo meio sem rumo, o A* tem uma sacada genial: ele usa uma fórmula mágica para decidir qual o próximo passo dar. Essa fórmula é a f(n) = g(n) + h(n), e eu explico já já o que significa cada pedacinho.
| Componente | Significado | Papel no A* |
|---|---|---|
| g(n) | Custo real do início até o nó atual | Mede o quão longe você já chegou. |
| h(n) | Custo estimado do nó atual até o destino (heurística) | É uma ‘previsão’ inteligente do caminho restante, geralmente a distância em linha reta. |
| f(n) | Custo total estimado (g(n) + h(n)) | O algoritmo sempre prioriza explorar o nó com o menor f(n), pois é a aposta mais promissora. |
A grande sacada é que, ao usar essa ‘estimativa’ (a heurística), o A* consegue focar a busca. Enquanto o Dijkstra, coitado, explora em ondas para todos os lados até achar o alvo, o A* tenta dar uma ‘miradinha’ na direção certa. E o mais bacana: se a sua heurística for ‘admissível’ (ou seja, nunca superestimar o custo real), o A* te garante o caminho mais curto. É segurança pura!
Ferramentas Essenciais para Implementar o Algoritmo A*
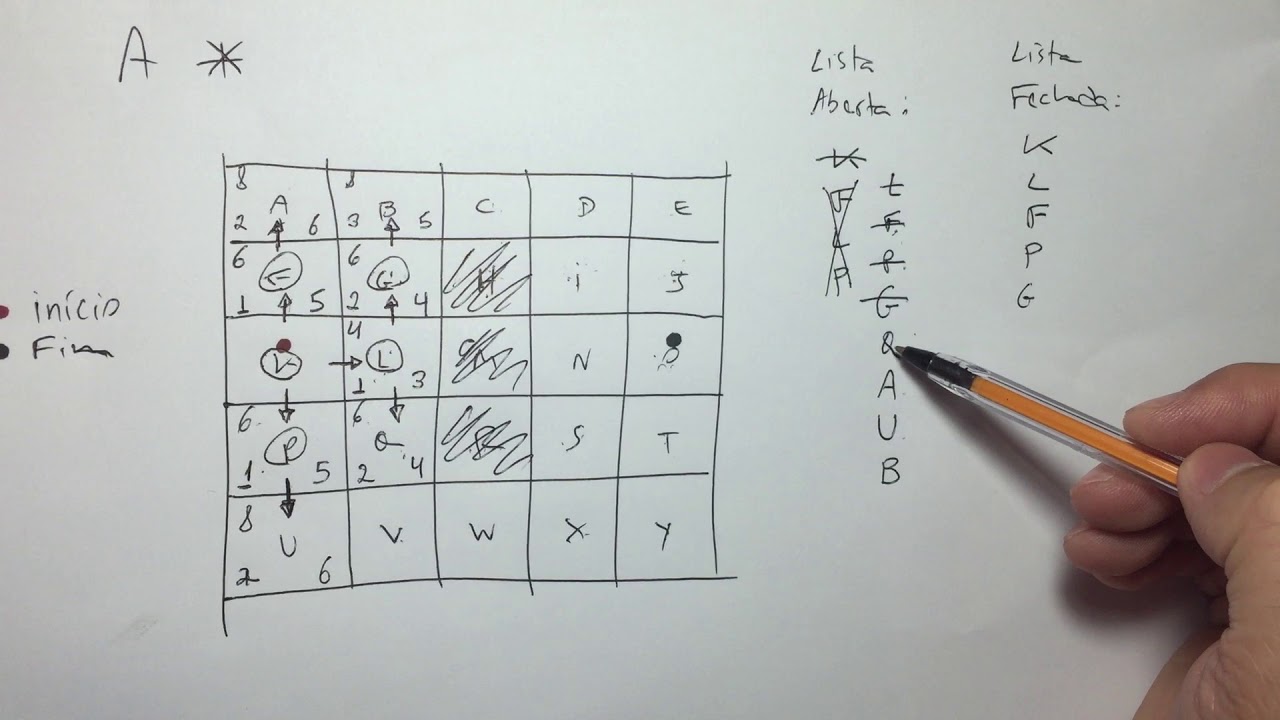
Python com Bibliotecas Especializadas

Para quem trabalha com Python, a vida fica bem mais fácil. Existem bibliotecas que já trazem o A* pronto para usar ou facilitam muito a implementação. Eu gosto bastante de usar o NetworkX. Ele não tem uma função A* nativa direta, mas a estrutura dele para grafos é sensacional e você consegue implementar o algoritmo sobre ela com uma clareza enorme. Ele é ótimo para modelar cenários complexos, como redes de ruas ou caminhos em um mapa digital. Vi ótimos exemplos de uso em algoritmos de caminho mais curto no NetworkX que me ajudaram demais.
C++ para Performance Crítica
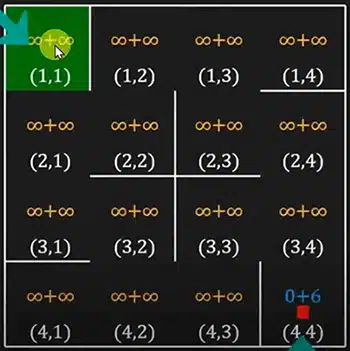
Agora, se você precisa de máxima performance, especialmente em jogos digitais ou robótica onde cada milissegundo conta, C++ é o caminho. Não tem biblioteca ‘mágica’ que faça tudo, mas a gente consegue implementar o A* de forma super otimizada. Pense em usar estruturas de dados eficientes, como um heap (ou priority queue) para gerenciar os nós a serem explorados. Esse controle fino é crucial para que o algoritmo não engasgue em cenários com muitos caminhos possíveis. Pesquisar sobre implementações de A* em C++ pode te dar um norte.
Ferramentas de Visualização de Grafos

Para entender de verdade como o A* funciona, nada como ver ele em ação. Existem ferramentas online e softwares que permitem visualizar a criação do grafo e a expansão dos nós. Isso é ouro! Ajuda a depurar o código e a pegar os ‘pulos’ que o algoritmo dá. Recomendo dar uma olhada em como funcionam as visualizações em sites que explicam o algoritmo A* na prática. Ajuda a pegar o jeito.
Implementações em Pseudocódigo e Tutoriais

Antes de sair codando, eu sempre recomendo dar uma olhada em pseudocódigo e tutoriais. Eles te mostram a lógica pura, sem se prender à sintaxe de uma linguagem específica. Sites como o GeeksforGeeks ou a documentação do jogo Red Blob Games oferecem ótimos materiais. Entender a base te poupa muita dor de cabeça depois.
Preparando o Terreno: O Que Você Precisa Saber Antes de Implementar o A*
Antes de mergulhar de cabeça na codificação do A*, é fundamental entender alguns conceitos-chave. Primeiro, você precisa ter uma representação clara do seu problema como um grafo. Isso significa definir os nós (pontos, locais) e as arestas (conexões entre eles), juntamente com os custos associados a cada aresta. Pense em um mapa de cidade: as ruas são as arestas, os cruzamentos são os nós, e a distância ou o tempo de percurso em cada rua é o custo. A escolha de uma boa heurística é o segundo ponto crucial. Ela precisa ser ‘admissível’, ou seja, nunca pode dar um valor maior que o custo real para chegar ao destino. A distância Euclidiana (em linha reta) é uma heurística clássica e admiráve
Como Implementar o Algoritmo A* Passo a Passo
-
Definição do Grafo e da Heurística
O primeiro passo é modelar o seu problema. Crie uma estrutura de dados que represente o grafo. Cada nó deve ter informações sobre suas conexões (vizinhos) e o custo para chegar a eles. Paralelamente, defina a função heurística (h(n)). Para um mapa 2D, a distância Euclidiana (linha reta) entre dois pontos (x1, y1) e (x2, y2) é dada por
sqrt((x2-x1)^2 + (y2-y1)^2). Essa é uma heurística admíssivel clássica. Se estiver usando um sistema de grade, a distância de Manhattan (soma das diferenças absolutas das coordenadas) também funciona muito bem. -
Inicialização das Estruturas de Dados
Você vai precisar de duas listas principais: a ‘Open List’ (ou lista de abertos) e a ‘Closed List’ (ou lista de fechados). A Open List guarda os nós que já foram descobertos mas ainda não totalmente explorados; ela geralmente é implementada como uma fila de prioridade, ordenada pelo valor de f(n). A Closed List armazena os nós que já foram completamente explorados, evitando que sejam visitados novamente. Inicialmente, a Open List contém apenas o nó de partida, com seu g(n) = 0 e h(n) calculado para o destino. A Closed List está vazia.
-
O Loop Principal de Busca
Enquanto a Open List não estiver vazia, retire o nó com o menor valor de f(n) dela. Este nó se torna o nó atual. Se este nó for o destino, parabéns! Você encontrou o caminho. Agora, é só reconstruir o trajeto voltando pelos ‘pais’ de cada nó. Caso contrário, adicione o nó atual à Closed List.
-
Exploração dos Vizinhos
Para cada vizinho do nó atual, se ele já estiver na Closed List, ignore-o. Caso contrário, calcule o custo g(n) para chegar a este vizinho através do nó atual. Se o vizinho não estiver na Open List, adicione-o, calcule seu f(n) (usando o g(n) recém-calculado e a heurística h(n)) e defina o nó atual como seu ‘pai’. Se o vizinho já estiver na Open List, verifique se o novo caminho (através do nó atual) é mais curto (tem um g(n) menor). Se for, atualize o g(n) do vizinho, seu f(n) e seu ‘pai’.
-
Reconstrução do Caminho
Quando o nó de destino é alcançado, o caminho é reconstruído de trás para frente. Comece pelo destino e vá seguindo o ‘pai’ de cada nó até chegar ao nó de partida. A sequência desses nós, na ordem inversa, é o caminho mais curto encontrado. Algumas implementações de GPS, como as baseadas em Google Maps, usam variações desse princípio.
Como Consertar Erros Comuns na Implementação do A*
Um erro clássico é usar uma heurística ‘não admissível’. Isso significa que sua função h(n) está estimando um custo maior do que o real para chegar ao destino. O resultado? O algoritmo pode falhar em encontrar o caminho mais curto ou até mesmo não encontrar um caminho que existe. Fique de olho em como sua heurística foi definida; ela deve ser conservadora. Outro ponto é a gestão da Open e Closed Lists. Se você não remover corretamente os nós da Open List ao processá-los ou não os adicionar à Closed List, pode acabar em loops infinitos ou revisitar nós desnecessariamente, comprometendo a performance e a correção. Lembra da garantia de otimização do A*? Ela só funciona com heurística admissível. Para aplicações de navegação robótica, por exemplo, garantir que essa condição seja atendida é vital, como descrito em estudos sobre algoritmos de planejamento de caminho. Outro erro comum é a reconstrução do caminho. Se você não armazenar corretamente os ‘pais’ de cada nó durante a exploração, não conseguirá traçar a rota final. Verifique se a lógica de atualização do pai está correta sempre que um caminho melhor para um nó é encontrado. Pense nisso como as dicas sobre diálogos em Java, que parecem simples, mas a lógica precisa estar impecável para funcionar.

